Bạn đang đọc: Các bài toán xác suất
Thí dụ $1$. Một tổ học sinh gồm $9$ em, trong các số đó có $3$ người vợ được chia thành $3$ nhóm gần như nhau. Tính tỷ lệ để từng nhóm bao gồm $1$ nữ.Lời giải. Gọi $A$ là trở nên cố : “ nghỉ ngơi $3$ nhóm học viên mỗi nhóm gồm $1$ nữ”.+ Để tìm $n(Omega)$ ta thực hiệnChọn đột nhiên $3$ vào $9$ em đưa vào nhóm sản phẩm công nghệ nhất, số năng lực là $C_9^3$.Chọn $3$ trong những $6$ em còn lại đưa vào nhóm lắp thêm hai, số tài năng là $C_6^3.$Chọn $3$ em gửi vào nhóm sản phẩm $3,$ số kỹ năng là $C_3^3=1.$Vậy $n(Omega) = C_9^3. C_6^3. 1=1680$.Vì phân tự dưng nên các biến số sơ cung cấp trong không gian biến núm sơ cấp này có cùng kĩ năng xuất hiện.Để tìm $n(A)$ ta triển khai Phân $3$ thiếu nữ vào $3$ team nên gồm $3!$ cách khác nhau.Phân $6$ nam vào $3$ nhóm theo cách như trên, ta có $C_6^2. C_4^2. 1$ giải pháp khác nhauSuy ra $n(A) = 3!.C_9^3. C_6^3. 1=540$.+ vì vậy $P(A)=displaystyle fracn(A)n(Omega)=displaystyle frac5401680=frac2784$DẠNG II. Tính xác suất bằng quy tắc cộngCách giải. thực hiện kỹ thuật đếm và những công thức sau để tính phần trăm của biến đổi cố đối, thay đổi cố hợp,$P(overlineA)=1-P(A); P(A cup B)=P(A)+P(B)$, nếu $A cap B= emptyset$.Thí dụ $2$: Một vỏ hộp đựng $8$ viên bi xanh cùng $4$ viên bi đỏ. Lấy bất chợt $3$ viên bi. Tính xác suất để a) mang được $3$ viên bi thuộc màu.b) rước được $3$ viên bi khác màu.c) rước được tối thiểu $2$ viên bi xanh.Lời giải: a) call $A$ là trở thành cố “ lấy được $3$ viên bi xanh”, $B$ là vươn lên là cố “ lấy được $3$ viên bi đỏ” với $H $ là phát triển thành cố “ mang được $3$ viên bi thuộc màu”. Ta bao gồm $H=A cup B$, vì $A$ cùng $B$ xung khắc đề xuất $P(H) = P(A) + P(B)$.Ta tất cả $P(A)=fracC_8^3C_12^3=frac1455; P(B)=fracC_4^3C_12^3=frac155$.Từ đó $P(H)=frac1455+frac155=frac311$.b) trở thành cố “ đem được $3$ viên bi khác màu” là phát triển thành cố $overlineH$, Vậy$P(overlineH)=1-P(H)=1-frac311=frac811$c) điện thoại tư vấn $C$ là biến cố mang được $2$ viên bi xanh và một viên bi đỏ” , K là trở nên cố “ lấy được tối thiểu $2$ viên bi xanh”. Ta tất cả $K=A cup C$ , vày $A$ cùng $C$ xung khắc, đề nghị $P(K) = P(A) + P(C)$Ta gồm $P(C)=fracC_8^2.C_4^1C_12^3=frac2855$Suy ra $P(K)=frac1455+frac2855=frac4255$DẠNG III. Tính phần trăm bằng nguyên tắc nhânCách giải.Xem thêm: U23 Việt Nam Tập Bài Chiến Thuật Cho Trận Giao Hữu Với U23 Kyrgyzstan Tối Nay
Để tính xác suất của biến chuyển cố giao của hai đổi mới cố chủ quyền $A$ cùng $B$ ta dùng cách làm $P(AB) =P(A)P(B)$Thí dụ $3$. Có hai hộp chứa các quả cầu. Hộp vật dụng thất cất $3$ quả ước trắng, $7$ quả ước đỏ cùng $15$ quả cầu xanh. Hộp thứ hai cất $10$ quả cầu trắng, $6$ quả cầu đỏ với $9$ quả ước xanh. Trường đoản cú mỗi hộp lấy bất chợt ra một quả ước . Tính xác suất để nhì quả cầu kéo ra có màu như là nhau. Giải mã : điện thoại tư vấn $A$ là đổi thay cố "Quả mong được lấy ra từ hộp thứ nhất là color trắng", $B$ là biến đổi cố "Quả cầu được lấy ra từ hộp đồ vật hai là color trắng".Ta gồm $P(A)=frac325, P(B)=frac1025$. Vậy xác suất để nhì quả cầu được mang ra đều màu trắng là $P(AB) = P(A) P(B) =frac325.frac1025=frac30625$( do $A, B$ độc lập)Tương tự, phần trăm để nhị quả mong được kéo ra đều màu xanh lá cây là $frac1525.frac925=frac135625$, với xác suất để đưa ra nhì quả cầu đều red color là $frac625.frac725=frac42625.$Theo luật lệ cộng, xác suất để mang ra nhì quả cầu cùng màu sắc là$frac30625+frac135625+frac42625=frac207625$.Dạng IV. Lập bảng phân bố phần trăm của vươn lên là ngẫunhiên tránh rạc.Cách giải : Để lập bảng phân bố xác suất của biến đột nhiên rời rốc $X$ ta thựchiện quá trình :+ xác định tập những giá trị rất có thể $left x_1,x_2,cdots,x_n ight$ của $X$.+ Tính các xác suất $p_i=P(X=x_i),$ trong số đó $left X=x_i ight$ là biếncố "$X$ nhận quý giá $x_i$".+ trình bày bảng phân bố xác suất theo dạng sau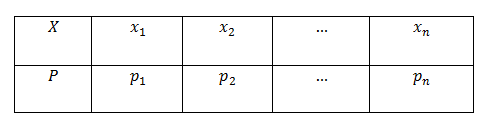
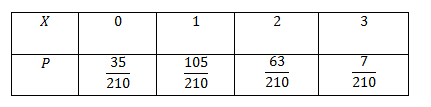
Ví dụ $4.$ Một lô hàng có $10$ sản phẩm trong đó tất cả $3$ sản phẩm xấu. Chọn ngẫunhiên cùng lúc $4$ sản phẩn để kiểm tra. điện thoại tư vấn $X$ là số thành phầm xấu chạm chán phảikhi kiểm tra. Lập bảng phân bố phần trăm của $X$.Lời giải :Dễ thấy $X$ nhận các giá trị thuộc tập $left 0,1,2,3 ight$. Ta bao gồm :$P(X=0)=fracC_7^4C_10^4=frac35210$$P(X=1)=fracC_3^1.C_7^3C_10^4=frac105210$$P(X=2)=fracC_3^2.C_7^2C_10^4=frac63210$$P(X=3)=fracC_3^3.C_7^1C_10^4=frac7210$Vậy bảng phân bố phần trăm của $X$ là