Tài liệu bao hàm các cách thức chứng minh bất đẳng thức từ bỏ cơ bạn dạng nhất mang lại kĩ thuật nâng cấp đặc sắc. Từng bài đều phải có phân tích cùng lời giải chi tiết rất hữu ích cho những em.
Bạn đang đọc: Sử dụng bất đẳng thức phụ chứng minh bất đẳng thức
Chương I. MỘT SỐ PHƯƠNG PHÁP GIẢI TOÁN
Chủ đề 1 Kỹ thuật chuyển đổi tương đương 3 chủ thể 2 sử dụng các tính chất của tỉ số, đặc thù giá trị hoàn hảo và tính chất của tam thức bậc nhì trong chứng tỏ bất đẳng thức 44 1. Sử dụng đặc điểm của tỉ số 45 2. Sử dụng đặc điểm giá trị tuyệt vời 54 3. Sử dụng đặc điểm tam thức bậc hai. 59 chủ thể 3 minh chứng bất đẳng thức bằng phương pháp phản hội chứng 68 chủ thể 4 minh chứng các bất đẳng thức về tổng, tích của hàng số - cách thức quy hấp thụ 86 chủ thể 5 Kỹ thuật sử dụng bất đẳng thức CAUCHY 117 1. Kỹ thuật chọn điểm rơi trong review từ trung bình cùng sang trung bình nhân 118 2. Kỹ thuật lựa chọn điểm rơi trong review từ trung bình nhân sang vừa phải cộng. 141 3. Nghệ thuật ghép cặp trong bất đẳng thức Cauchy 161 4. Chuyên môn thêm bớt 175 5. Kỹ thuật Cauchy ngược dấu 191 6. Nghệ thuật đổi trở nên số 199 chủ thể 6 Kỹ thuật áp dụng bất đẳng thức BUNHIACOPXKI 220 1. Kỹ thuật chọn điểm rơi 221 2. Kỹ thuật sử dụng bất đẳng thức Bunhiacopxki dạng cơ bạn dạng 236 3. Kỹ thuật sử dụng bất đẳng thức Bunhiacopxki dạng phân thức 252 4. Chuyên môn thêm giảm 275 5. Chuyên môn đổi trở thành trong bất đẳng thức Bunhiacopxki 289
Chương II. MỘT SỐ KỸ THUẬT GIẢI TOÁN ĐẶC SẮC chủ đề 7 Ứng dụng nguyên lý DIRICHLET trong chứng tỏ bất đẳng thức 307 chủ đề 8 phương pháp hệ số cô động trong chứng tỏ bất đẳng thức 319 chủ thể 9 Ứng dụng một hệ trái của bất đẳng thức SCHUR 333 chủ đề 10 Ứng dụng của đạo hàm trong chứng minh bất đẳng thức và việc 344
tìm cực trị. 1. Dồn vươn lên là nhờ áp dụng kỹ thuật sử dụng các bất đẳng thức bom tấn 344 2. Dồn phát triển thành nhờ kết phù hợp với kỹ thuật đổi phát triển thành số. 367 3. Dồn trở thành nhờ kết phù hợp với kỹ thuật sắp đến thứ tự những biến 382 4. Phương thức tiếp đường 389 5. Khảo sát hàm nhiều thay đổi số 393 6. Kết phù hợp với việc sử dụng Bổ đề 398 7. Vận dụng kỹ thuật dồn biến cổ điển 405
Xem thêm: Đèn Ngủ Tân Cổ Điển Giá Rẻ Nhiều Mẫu Đẹp Chất Lượng Cao, Đèn Bàn Tân Cổ Điển Mb3048
Chương III. TUYỂN CHỌN MỘT SỐ BÀI TOÁN BẤT ĐẲNG THỨC chủ đề 11 một trong những bất đẳng thức giỏi và khó khăn 409 chủ đề 12 một vài bất đẳng thức trong số đề thi học sinh giỏi, thi TSĐH cùng tuyển sinh lớp 10 siêng toán. 649
MỘT SỐ KIẾN THỨC CƠ BẢN VỀ BẤT ĐẲNG THỨC I. Định nghĩaGiả sử A với B là nhị biểu thức thông qua số hoặc bởi chữ. Khi đó +) (A > B;A + (A - B > 0;A - B + Một bất đẳng thức bất kì hoàn toàn có thể đúng, cũng rất có thể sai. Quy ước: Khi nói đến một bất đẳng thức cơ mà không nói gì thêm thì ta gọi đó là một trong bất đẳng thức đúng.

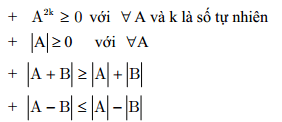
Chương I – MỘT SỐ PHƯƠNG PHÁP CHỨNG MINH BẤT ĐẲNG THỨCNội dung cơ phiên bản của chương I gồm: · ra mắt các phương thức chứng minh bất đẳng thức. · Nêu một số trong những tính chất liên quan, một số lưu ý của các phương thức chứng minh bất đẳng thức trên. · ra mắt các bài bác tập mẫu mã cùng quá trình phân tích, suy luận để tìm ra các giải mã và các giải mã được trình bày cụ thể. · giới thiệu một số bài xích tập tự luyện.


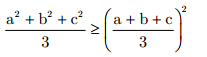











Tải về
Luyện bài xích tập trắc nghiệm môn Toán lớp 10 - xem ngay






