Các Công Thức Tính Lim

Cách tính lim bằng tay thủ công của hàm số trong bài viết này của shop chúng tôi sẽ góp bạn hối hả giải được những bài xích toán giới hạn tính lim bằng cách thức thủ công

Hãy đọc kỹ bài viết này và vứt túi các cách giải lim nhanh chóng, dễ dàng trong nội dung bài viết này của shop chúng tôi nhé !

Tham khảo nội dung bài viết khác:

biện pháp giải Lim bằng tay thủ công đơn giản

1.

Bạn đang đọc: Các công thức tính lim

Dạng 0/0 so với giới hạn tại một điểm

Ví dụ 1: 

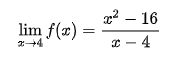
+) cách 1: Ta thay 4 vào phương trình f(x) thì sẽ tiến hành dạng 0/0 cần khẳng định đấy là dạng 0/0

+) bước 2: biến đổi đổi:

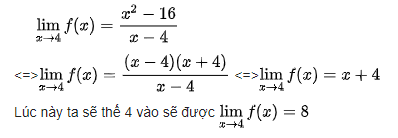
2.

+) ví dụ 1: Dạng đã biến đổi

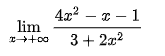
Lúc này ta thấy số mũ lớn nhất của tử và mẫu mã là x^2, vị vậy ta sẽ phân tách cả tử với mẫu mang lại x^2

 +) ví dụ 2: Dạng chưa trở thành đổi

3. Dạng ∞; – ∞  : Ta sẽ nhân lượng liên hợp

Ví dụ 1: 

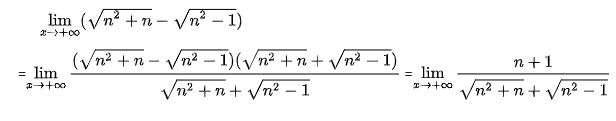
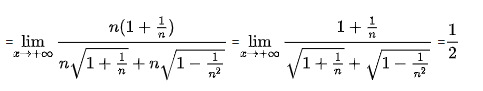
4.

Xem thêm: Ghế Ngồi Ăn Cho Trẻ - (Review) +5 Ghế Ăn Dặm Cho Bé Loại Nào Tốt Nhất

Dạng 0.∞: Ta biến hóa về dạng ∞/∞ hoặc 0/0

– ví dụ như minh họa:

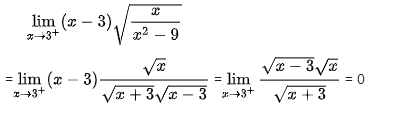
một số trong những cách tính Lim thủ công bằng tay khác

1. Thực hiện định nghĩa tìm số lượng giới hạn 0 của hàng số

2. Tìm số lượng giới hạn của hàng số bởi công thức

– một trong những công thức ta thường gặp gỡ khi tính giới hạn hàm số như sau:

3. Thực hiện định nghĩa tìm giới hạn hữu hạn

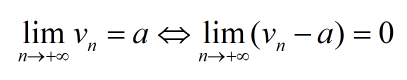
4. Sử dụng những giới hạn đặc trưng cùng cùng với định lý để xử lý các câu hỏi tìm số lượng giới hạn dãy số

+) Ta thường sử dụng những dạng giới hạn:

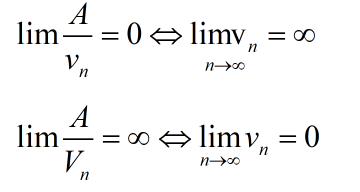
+) nếu như biểu thức bao gồm dạng phân thức tử số và chủng loại số chứa lũy quá của n thì ta triển khai chia cả tử và mẫu đến n^k với k là mũ tối đa ở bậc mẫu.

+) trường hợp biểu thức cất căn thức phải nhân một lượng liên hợp để đưa về dạng cơ bản thì ta có một trong những lượng liên hợp cần thiết

Cám ơn các bạn đã theo dõi bài viết này của chúng tôi, chúc bạn thành công xuất sắc và may mắn !